Paul HONEINE - The Pre-image Problem in Machine Learning -

Paul HONEINE

- The Pre-image Problem in Machine Learning -

The Pre-image Problem

Kernel machines have gained considerable popularity during the last fifteen years, making a breakthrough in nonlinear signal processing and machine learning thanks to extraordinary advances. This increased interest is undoubtedly driven by the practical goal of being able to easily develop efficient nonlinear algorithms. The key principle behind this, known as the kernel trick, exploits the fact that a great number of data processing techniques do not depend explicitly on the data itself, but rather on a similarity measure between them, i.e., an inner product. To provide a nonlinear extension of these techniques, one can apply a nonlinear transformation to the data, mapping them into some feature space. According to the kernel trick, this can be achieved by simply replacing the inner product with a reproducing kernel (i.e., positive semi-definite symmetric function), the latter corresponds to an inner product in the feature space. One consequence is that the resulting nonlinear algorithms show significant performance improvements over their linear counterparts, with essentially the same computational complexity.

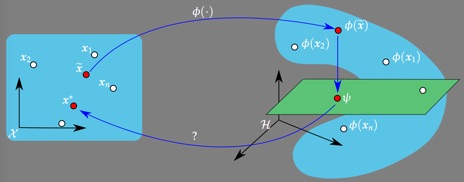
While the nonlinear mapping from the input space to the feature space is central in kernel methods, the reverse mapping from the feature space back to the input space is also of primary interest. This is the case in many applications, including kernel principal component analysis for signal and image denoising. Unfortunately, it turns out that the reverse mapping generally does not exist, and only a few elements in the feature space have a valid pre-image in the input space. The so-called pre-image problem consists of finding an approximate solution, by identifying data in the input space based on their corresponding features in the high-dimensional feature space.

In the following, we shall provide a brief summary of the work done since 2008, as well as ongoing work. Our main contributions are threefold:

1.We have provided theoretical studies to better understand the pre-image problem and have proposed relevant solutions. This is the case for instance of the proposed conformal map, and solving under the nonnegativity constraint.
2.We have demonstrated that the resolution of the pre-image problem opens the way for new classes of nonlinear methods, by extending the scope of kernel-based machines. Of particular interest are:
•Time series analysis with kernel-based autoregressive models.
•Auto-localization in wireless sensors networks.
•Feature extraction in signal and image processing.
•Spectral unmixing in hyperspectral imaging
3.We have recently studied the problem of nonnegative matrix factorization (NMF), by providing a kernel-based NMF that does not suffer from the curse of the pre-image.

Kernel-based Nonnegative Matrix Factorization (2013-2017):

(Recent Work of PhD Student Fei Zhu)

THE nonnegative matrix factorization (NMF) has become a prominent analysis technique in many fields, owing to its power to extract sparse and tractable interpretable representations from a given data matrix. The scope of application spans feature extraction, compression and visualization, within pattern recognition, machine learning, and signal and image processing. It has been popularized since Lee and Seung discovered that, when applied to an image, “NMF is able to learn the parts of objects”. Since then, NMF has been successfully applied in image classification, face expression recognition, audio analysis, objet recognition, clustering, and many bioinformatics applications, including computational biology and gene expression data. Moreover, the NMF is tightly connected to spectral clustering.

A great challenge arises when dealing with a nonlinear formulation of the NMF. Within the framework of kernel machines, the models suggested in the literature do not allow the representation of the factorization matrices, which is a fallout of the curse of the pre-image. In our work, we propose a novel kernel-based model for the NMF that does not suffer from the pre-image problem, by investigating the estimation of the factorization matrices directly in the input space. Within the proposed framework, we develop several extensions to incorporate constraints, including sparseness, smoothness, and spatial regularization with a total-variation-like penalty.

Online Kernel NMF:

Combining the linear and the Kernel NMF:

Time Series Analysis and Modeling with Kernel AutoRegressive Models (2011-2013):

This work proposes nonlinear autoregressive (AR) models for time series, within the framework of kernel machines. Several models are investigated. Essentially, the AR model is defined on the mapped samples in the feature space. In order to predict a future sample, this formulation requires to solve a pre-image problem to get back to the input space. We also propose a novel model that attempts by bypass the pre-image problem, by defining the AR model with an hybrid model, as a tradeoff considering the computational time and the precision. The model’s parameters are estimated using techniques such as the Yule-Walker equations, under the stationarity assumption.

Pre-imaging Under the Nonnegativity Constraint (2010-2013):

Rules of physics in many real-life problems force some constraints to be satisfied. This work deals with nonlinear pattern recognition under non-negativity constraints. While kernel principal component analysis can be applied for feature extraction or data denoising, in a feature space associated to the considered kernel function, a pre-image technique is required to go back to the input space, e.g., representing a feature in the space of input signals. The main purpose of our work is to study a constrained pre-image problem with non-negativity constraints. We provide new theoretical results on the pre-image problem, including the weighted combination form of the pre-image, and demonstrate sufficient conditions for the convexity of the problem. The constrained problem is considered with the non-negativity, either on the pre-image itself or on the weights. We propose appropriate techniques to incorporate these constraints. A fortuitous side-effect of our approach is the sparsity in the representation, a property investigated in detail.

Unmixing in Hyperspectral Imagery (2012-2013):

Spectral unmixing is an important issue to analyze remotely sensed hyperspectral data. This involves the decomposition of each mixed pixel into its pure endmember spectra, and the estimation of the abundance value for each endmember. Although linear mixture models are often considered because of their simplicity, there are many situations in which they can be advantageously replaced by nonlinear mixture models. In this work, we derive a supervised kernel-based unmixing method that relies on a pre-image problem-solving technique. The kernel selection problem is also briefly considered. We show that partially-linear kernels can serve as an appropriate solution, and the nonlinear part of the kernel can be advantageously designed with manifold-learning-based techniques. We also incorporate spatial information into our method in order to improve unmixing performance.

Localization in Wireless Sensor Networks as a Pre-image Problem (2007-2011):

For details on the localization problem, see page Indoor GeoLocalization in Wireless Sensor Networks.

Advances in the Resolution of the Pre-image Problem (2009-2012):

Online Resolution of the Pre-image Problem:

Surveys on the Pre-image Problem and its Resolution:

The Conformal Map Approach for Solving the Pre-image Problem:

- The Pre-image Problem in Machine Learning -

PhD Students:

Fei Zhu (2013-2016)

Maya Kallas (2009-2012, now Assistant Prof.)

PhD Students (Partially Associated):

Nguyen Hoang Nguyen (2010-2013)

Mehdi Essoloh (2006-2009, now at DGA)