PhD Students:
Fei Zhu (2013-2016)
Maya Kallas (2009-2012, now Assistant Prof.)
PhD Students (Partially Associated):
Nguyen Hoang Nguyen (2010-2013)
Mehdi Essoloh (2006-2009, now at DGA)
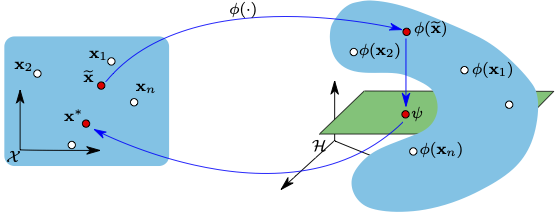
The Pre-image Problem
Kernel machines have gained considerable popularity during the last fifteen years, making a breakthrough in nonlinear signal processing and machine learning thanks to extraordinary advances. This increased interest is undoubtedly driven by the practical goal of being able to easily develop efficient nonlinear algorithms. The key principle behind this, known as the kernel trick, exploits the fact that a great number of data processing techniques do not depend explicitly on the data itself, but rather on a similarity measure between them, i.e., an inner product. To provide a nonlinear extension of these techniques, one can apply a nonlinear transformation to the data, mapping them into some feature space. According to the kernel trick, this can be achieved by simply replacing the inner product with a reproducing kernel (i.e., positive semi-definite symmetric function), the latter corresponds to an inner product in the feature space. One consequence is that the resulting nonlinear algorithms show significant performance improvements over their linear counterparts, with essentially the same computational complexity.
While the nonlinear mapping from the input space to the feature space is central in kernel methods, the reverse mapping from the feature space back to the input space is also of primary interest. This is the case in many applications, including kernel principal component analysis for signal and image denoising. Unfortunately, it turns out that the reverse mapping generally does not exist, and only a few elements in the feature space have a valid pre-image in the input space. The so-called pre-image problem consists of finding an approximate solution, by identifying data in the input space based on their corresponding features in the high-dimensional feature space.
In the following, we shall provide a brief summary of the work done since 2008, as well as ongoing work. Our main contributions are threefold:
1. We have provided theoretical studies to better understand the pre-image problem and have proposed relevant solutions. This is the case for instance of the proposed conformal map, and solving under the nonnegativity constraint.
2. We have demonstrated that the resolution of the pre-image problem opens the way for new classes of nonlinear methods, by extending the scope of kernel-based machines. Of particular interest are:
• Time series analysis with kernel-based autoregressive models.
• Auto-localization in wireless sensors networks.
• Feature extraction in signal and image processing.
• Spectral unmixing in hyperspectral imaging
3. We have recently studied the problem of nonnegative matrix factorization (NMF), by providing a kernel-based NMF that does not suffer from the curse of the pre-image.
Kernel-based Nonnegative Matrix Factorization (2013-2020)
(Work of PhD Student Fei Zhu)
The nonnegative matrix factorization (NMF) has become a prominent analysis technique in many fields, owing to its power to extract sparse and tractable interpretable representations from a given data matrix. The scope of application spans feature extraction, compression and visualization, within pattern recognition, machine learning, and signal and image processing. It has been popularized since Lee and Seung discovered that, when applied to an image, “NMF is able to learn the parts of objects”. Since then, NMF has been successfully applied in image classification, face expression recognition, audio analysis, objet recognition, clustering, and many bioinformatics applications, including computational biology and gene expression data. Moreover, the NMF is tightly connected to spectral clustering.
A great challenge arises when dealing with a nonlinear formulation of the NMF. Within the framework of kernel machines, the models suggested in the literature do not allow the representation of the factorization matrices, which is a fallout of the curse of the pre-image. In our work, we propose a novel kernel-based model for the NMF that does not suffer from the pre-image problem, by investigating the estimation of the factorization matrices directly in the input space. Within the proposed framework, we develop several extensions to incorporate constraints, including sparseness, smoothness, and spatial regularization with a total-variation-like penalty.
Fei Zhu, Paul Honeine, and Maya Kallas
Kernel non-negative matrix factorization without the pre-image problem.
Proc. 24th IEEE workshop on Machine Learning for Signal Processing (MLSP), Reims, France, pp. 1-6, 21-24 Sept., 2014
Fei Zhu and Paul Honeine
Online Kernel Nonnegative Matrix Factorization.
Signal Processing, 131:143 – 153, Feb. 2017.
Fei Zhu and Paul Honeine
Online nonnegative matrix factorization based on kernel machines.
Proc. 23rd European Conference on Signal Processing (EUSIPCO), Nice, France, pp. 2381-2385, 31 Aug.-4 Sept., 2015
Paul Honeine and Fei Zhu
Eviter la malédiction de pré-image : application à la factorisation en matrices non négatives à noyaux.
Actes du 25-ème Colloque GRETSI sur le Traitement du Signal et des Images (GRETSI’15), Lyon, France, Sept., 2015
Combining the linear and the Kernel NMF
Fei Zhu and Paul Honeine
Bi-objective Nonnegative Matrix Factorization: Linear Versus Kernel-based Models.
IEEE Transactions on Geoscience and Remote Sensing, 54 (7) , pp. 4012-4022, July, 2016
Fei Zhu and Paul Honeine
Pareto front of bi-objective kernel-based nonnegative matrix factorization.
Proc. 23rd Europ. Symp. on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN, ISBN: 978-287587014-8), Bruges, Belgium, pp. 585-590, 22-24 April, 2015
Time Series Analysis and Modeling with Kernel AutoRegressive Models (2011-2013)
This work proposes nonlinear autoregressive (AR) models for time series, within the framework of kernel machines. Several models are investigated. Essentially, the AR model is defined on the mapped samples in the feature space. In order to predict a future sample, this formulation requires to solve a pre-image problem to get back to the input space. We also propose a novel model that attempts by bypass the pre-image problem, by defining the AR model with an hybrid model, as a tradeoff considering the computational time and the precision. The model’s parameters are estimated using techniques such as the Yule-Walker equations, under the stationarity assumption.
Maya Kallas, Paul Honeine, Clovis Francis, and Hassan Amoud
Kernel autoregressive models using Yule-Walker equations.
Signal Processing, 93 (11), pp. 3053-3061, Nov., 2013
Maya Kallas, Paul Honeine, Cédric Richard, Clovis Francis, and Hassan Amoud
Prediction of time series using Yule-Walker equations with kernels.
Proc. 37th IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, pp. 2185-2188, 25-30 March, 2012
Maya Kallas, Paul Honeine, Cédric Richard, Clovis Francis and Hassan Amoud
Modèle autorégressif non-linéaire à noyau. Une première approche.
Actes du 23-ème Colloque GRETSI sur le Traitement du Signal et des Images (GRETSI’11), Bordeaux, France, Sept., 2011
Maya Kallas, Paul Honeine, Cédric Richard, Clovis Francis and Hassan Amoud
Kernel-Based Autoregressive Modeling with a Pre-Image Technique.
Proc. IEEE workshop on Statistical Signal Processing (SSP), Nice, France, pp. 281-284,28-30 June, 2011
Pre-imaging Under the Nonnegativity Constraint (2010-2013)
Rules of physics in many real-life problems force some constraints to be satisfied. This work deals with nonlinear pattern recognition under non-negativity constraints. While kernel principal component analysis can be applied for feature extraction or data denoising, in a feature space associated to the considered kernel function, a pre-image technique is required to go back to the input space, e.g., representing a feature in the space of input signals. The main purpose of our work is to study a constrained pre-image problem with non-negativity constraints. We provide new theoretical results on the pre-image problem, including the weighted combination form of the pre-image, and demonstrate sufficient conditions for the convexity of the problem. The constrained problem is considered with the non-negativity, either on the pre-image itself or on the weights. We propose appropriate techniques to incorporate these constraints. A fortuitous side-effect of our approach is the sparsity in the representation, a property investigated in detail.
Maya Kallas, Paul Honeine, Cédric Richard, Clovis Francis, and Hassan Amoud
Non-negativity constraints on the pre-image for pattern recognition with kernel machines.
Pattern Recognition, 46 (11) , pp. 3066-3080, Nov., 2013
Maya Kallas, Paul Honeine, Hassan Amoud and Clovis Francis
Sur le problème de la pré-image en reconnaissance des formes avec contraintes de non-négativité.
Actes du 23-ème Colloque GRETSI sur le Traitement du Signal et des Images (GRETSI’11), Bordeaux, France, Sept., 2011
Maya Kallas, Paul Honeine, Cédric Richard, Clovis Francis, and Hassan Amoud
Non-Negative Pre-Image in Machine Learning for Pattern Recognition.
Proc. 19th European Conference on Signal Processing (EUSIPCO), Barcelona, Spain, 29 Aug.-2 Sept., 2011
Maya Kallas, Paul Honeine, Cédric Richard, Hassan Amoud, and Clovis Francis
Nonlinear feature extraction using kernel principal component analysis with non-negative pre-image.
Proc. 32nd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Buenos Aires, Argentina, pp. 3642-3645, 31 Aug.-4 Sept.,2010
Unmixing in Hyperspectral Imagery (2012-2013)
Spectral unmixing is an important issue to analyze remotely sensed hyperspectral data. This involves the decomposition of each mixed pixel into its pure endmember spectra, and the estimation of the abundance value for each endmember. Although linear mixture models are often considered because of their simplicity, there are many situations in which they can be advantageously replaced by nonlinear mixture models. In this work, we derive a supervised kernel-based unmixing method that relies on a pre-image problem-solving technique. The kernel selection problem is also briefly considered. We show that partially-linear kernels can serve as an appropriate solution, and the nonlinear part of the kernel can be advantageously designed with manifold-learning-based techniques. We also incorporate spatial information into our method in order to improve unmixing performance.
Nguyen Hoang Nguyen, Jie Chen, Cédric Richard, Paul Honeine, and Céline Theys
Supervised nonlinear unmixing of hyperspectral images using a pre-image method.
New Concepts in Imaging: Optical and Statistical Models. In Eds. D. Mary, C. Theys, and C. Aime, EAS Publications Series, EDP Sciences, pp. 417-437, 2013
Localization in Wireless Sensor Networks as a Pre-image Problem (2007-2011)
For details on the localization problem, see page Indoor GeoLocalization in Wireless Sensor Networks.
Paul Honeine and Cédric Richard
Preimage problem in kernel-based machine learning.
IEEE Signal Processing Magazine, 28 (2), 77-88, March, 2011
Paul Honeine, Cédric Richard, and Hichem Snoussi
Auto-localisation dans les réseaux de capteurs sans fil par régression de matrices de Gram.
Actes du 22-ème Colloque GRETSI sur le Traitement du Signal et des Images, Dijon, France, Sept., 2009
Mehdi Essoloh, Cédric Richard, Hichem Snoussi, and Paul Honeine
Distributed localization in wireless sensor networks as a pre-image problem in a reproducing kernel Hilbert space.
Proc. 16th European Conference on Signal Processing (EUSIPCO), Lausanne, Switzerland, pp. 1-5, Aug. 2008
Paul Honeine, Cédric Richard, Mehdi Essoloh, and Hichem Snoussi
Localization in sensor networks – A matrix regression approach.
Proc. 5th IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM), Darmstadt, Germany, pp. 284-287, July 2008
Advances in the Resolution of the Pre-image Problem (2009-2012)
Online Resolution of the Pre-image Problem:
Paul Honeine
Online kernel principal component analysis: a reduced-order model.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 34 (9) , pp. 1814-1826, Sept., 2012
Surveys on the Pre-image Problem and its Resolution:
Paul Honeine and Cédric Richard
Preimage problem in kernel-based machine learning.
IEEE Signal Processing Magazine, 28 (2) , pp. 77-88, March, 2011
Maya Kallas, Paul Honeine, Clovis Francis and Hassan Amoud
A Comparative Study Of Pre-Image Techniques: The Kernel Autoregressive Case.
Proc. IEEE workshop on Signal Processing Systems (SiPS), Beirut, Lebanon, pp. 379-384, 4-7 Oct., 2011
The Conformal Map Approach for Solving the Pre-image Problem:
Paul Honeine and Cédric Richard
A closed-form solution for the pre-image problem in kernel-based machines.
Journal of Signal Processing Systems, 65 (3) Springer, New York, pp. 289-299, Dec., 2011
Paul Honeine and Cédric Richard
Solving the pre-image problem in kernel machines: a direct method.
Proc. 19th IEEE workshop on Machine Learning for Signal Processing (MLSP), Grenoble, France, pp. 1-6, September, 2009
BEST PAPER AWARD AT IEEE MLSP