Paul HONEINE

- Relative Stationarity Testing -

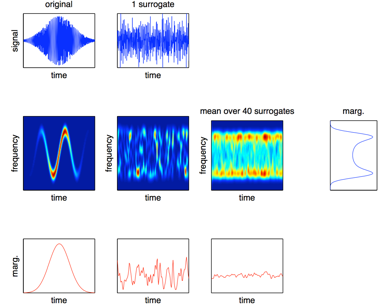
An operational framework is developed for testing stationarity of any signal relatively to an observation scale. The originality is to extract time-frequency features from a set of stationarized surrogate signals, and to use them for defining the null hypothesis of stationarity.

The surrogate data technique generates a family of stationarized signals, by destroying the time-varying structures in the signal phase while keeping its spectrum unchanged. In practice, this is achieved by keeping unchanged the magnitude of X(f), the Fourier transform of the initial signal x(t), and replacing its phase by a i.i.d. one. This leads to as many stationary surrogate signals as phase randomizations are operated.

The originality is to make use of the family of stationary surrogate signals for defining the null hypothesis of stationarity and, based upon this information, to derive statistical tests. Many contributions have been proposed, mainly by the use of machine learning.

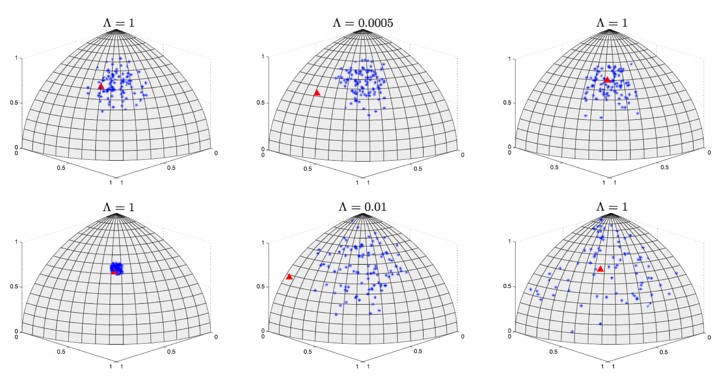
Figure: Spherical 3D representation of the surrogates (blue stars ∗) and the tested signal (red triangle), for the Amplitude Modulation (first row) and the Frequency Modulation (second row).

Left: The signal contains a great number of oscillations; Periodicity indicates a stationary regime.

Middle: Only one oscillation is available. The signal is considered as nonstationary.

Right: With a small portion of a period, there is no change in the amplitude or the frequency. It is considered as a stationary signal.

The proposed measure of stationarity of the signal under investigation is Λ, with the corresponding score given on top of each representation. Score Λ takes on a value of one if the signal x(t) under study is stationary and, the closer it is to zero, the greater the contrast between x(t) and the surrogates is.

Some Related Publications

P. BORGNAT, P. Flandrin, P. HONEINE, C. RICHARD, and J. XIAO
Testing Stationarity with Surrogates: A Time-Frequency Approach

IEEE Trans. on Signal Processing
58 (7) : 3459--3470, July 2010.

[paper] [bibTeX]

C. RICHARD, A. FERRARI, H. AMOUD, P. HONEINE, P. FLANDRIN, and P. BORGNAT
Statistical hypothesis testing with time-frequency surrogates to check signal stationarity

1. Proc. of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP)
   Dallas (Texas), 14 - 19 March, 2010.
   [paper] [bibTeX]
   

H. AMOUD, P. HONEINE, C. RICHARD, P. BORGNAT, and P. FLANDRIN
Time-Frequency Learning Machines For Nonstationarity Detection Using Surrogates

Proc. of IEEE Statistical Signal Processing Workshop (SSP)
Cardiff (Wales), UK, 31 Aug. - 3 Sept., 2009.
[paper] [bibTeX]

H. AMOUD, C. RICHARD, P. HONEINE, P. FLANDRIN, et P. BORGNAT
Sur la caractérisation de non-stationnarités par la méthode des substituts

Actes du 22-ème colloque GRETSI : Traitement du signal et des images
Dijon, France, 8 - 11 Sept. 2009.
[paper] [bibTeX]